Example V1-3 :  This is a case where we have one simple exponential part and 2 conjugated 3x3 (mu=1, d=1, r=1)+(mu=1, d=2, r=1). 

 

> A := rtable(1 .. 3, 1 .. 3, [[`/`(1, `*`(`^`(x, 4))), `/`(1, `*`(`^`(x, 3))), `/`(1, `*`(`^`(x, 2)))], [`/`(1, `*`(`^`(x, 3))), `/`(1, `*`(`^`(x, 5))), `/`(1, `*`(`^`(x, 4)))], [`/`(1, `*`(`^`(x, 5)))...
 

> Exp_part(A, x, t)
 

 

 

 

 

 

 

 

 

 

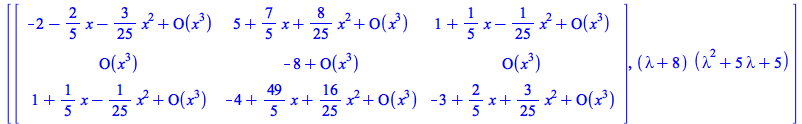[rtable(1 .. 3, 1 .. 3, [[`+`(`-`(2), `-`(`*`(`/`(2, 5), `*`(x))), `-`(`*`(`/`(3, 25), `*`(`^`(x, 2)))), O(`*`(`^`(x, 3)))), `+`(5, `*`(`/`(7, 5), `*`(x)), `*`(`/`(8, 25), `*`(`^`(x, 2))), O(`*`(`^`(x...
The first few terms of the transformation P in C((x)):
The first few terms of the transformation P in C((x)):
The first few terms of the transformation P in C((x)):
The first few terms of the transformation P in C((x)):
The first few terms of the transformation P in C((x)):
List of subsystem up to conjugaison after a first maximal Decomposition in C((x)):
List of subsystem up to conjugaison after a first maximal Decomposition in C((x)):
List of subsystem up to conjugaison after a first maximal Decomposition in C((x)):
List of subsystem up to conjugaison after a first maximal Decomposition in C((x)):
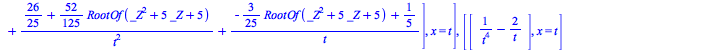[rtable(1 .. 1, 1 .. 1, [[`+`(`/`(`*`(`+`(3, RootOf(`+`(`*`(`^`(_Z, 2)), `*`(5, `*`(_Z)), 5)))), `*`(`^`(t, 5))), `-`(`/`(`*`(`/`(1, 5), `*`(RootOf(`+`(`*`(`^`(_Z, 2)), `*`(5, `*`(_Z)), 5)))), `*`(`^`...
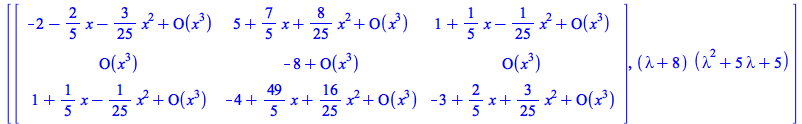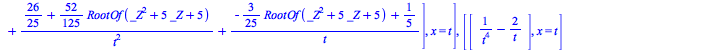[rtable(1 .. 1, 1 .. 1, [[`+`(`/`(`*`(`+`(3, RootOf(`+`(`*`(`^`(_Z, 2)), `*`(5, `*`(_Z)), 5)))), `*`(`^`(t, 5))), `-`(`/`(`*`(`/`(1, 5), `*`(RootOf(`+`(`*`(`^`(_Z, 2)), `*`(5, `*`(_Z)), 5)))), `*`(`^`...		 (9.1)
 

>
 

>