Example V1-5 : This is a case where we have one simple exponential part and a ramification of degree2 3x3 (mu=1,d=1,r=1)+(mu=1,d=1,r=2)
| > | ![A := rtable(1 .. 3, 1 .. 3, [[`/`(1, `*`(`^`(x, 4))), `/`(1, `*`(`^`(x, 3))), `/`(1, `*`(`^`(x, 4)))], [`/`(1, `*`(`^`(x, 4))), `/`(1, `*`(`^`(x, 4))), `/`(1, `*`(`^`(x, 5)))], [`/`(1, `*`(`^`(x, 5)))...](images/FormalReductionMapleExamples_392.gif) |
| > |
![[rtable(1 .. 3, 1 .. 3, [[`+`(`-`(`*`(16, `*`(`^`(x, 2)))), 6, O(`*`(`^`(x, 5)))), `+`(`-`(`*`(16, `*`(x))), O(`*`(`^`(x, 3)))), O(`*`(`^`(x, 3)))], [`+`(`-`(`*`(16, `*`(x))), O(`*`(`^`(x, 3)))), `+`(...](images/FormalReductionMapleExamples_396.gif) |
|
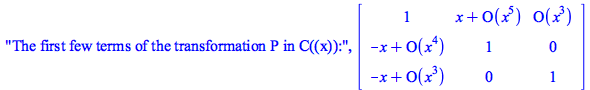 |
|
![[rtable(1 .. 1, 1 .. 1, [[`+`(`/`(1, `*`(`^`(t, 4))), `-`(`/`(1, `*`(`^`(t, 3)))), `-`(`/`(1, `*`(`^`(t, 2)))), `/`(1, `*`(t)))]], subtype = Matrix), x = t], [`+`(`/`(1, `*`(`^`(t, 11))), `/`(1, `*`(`...](images/FormalReductionMapleExamples_405.gif) |
(11.1) |
| > |
Example V1-5 : This is a case where we have one simple exponential part and a ramification of degree2 3x3 (mu=1,d=1,r=1)+(mu=1,d=1,r=2)
| > | ![A := rtable(1 .. 3, 1 .. 3, [[`/`(1, `*`(`^`(x, 4))), `/`(1, `*`(`^`(x, 3))), `/`(1, `*`(`^`(x, 4)))], [`/`(1, `*`(`^`(x, 4))), `/`(1, `*`(`^`(x, 4))), `/`(1, `*`(`^`(x, 5)))], [`/`(1, `*`(`^`(x, 5)))...](images/FormalReductionMapleExamples_392.gif) |
| > |
![[rtable(1 .. 3, 1 .. 3, [[`+`(`-`(`*`(16, `*`(`^`(x, 2)))), 6, O(`*`(`^`(x, 5)))), `+`(`-`(`*`(16, `*`(x))), O(`*`(`^`(x, 3)))), O(`*`(`^`(x, 3)))], [`+`(`-`(`*`(16, `*`(x))), O(`*`(`^`(x, 3)))), `+`(...](images/FormalReductionMapleExamples_396.gif) |
|
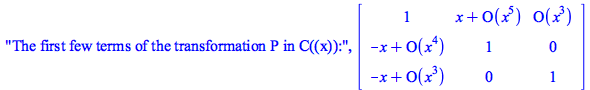 |
|
![[rtable(1 .. 1, 1 .. 1, [[`+`(`/`(1, `*`(`^`(t, 4))), `-`(`/`(1, `*`(`^`(t, 3)))), `-`(`/`(1, `*`(`^`(t, 2)))), `/`(1, `*`(t)))]], subtype = Matrix), x = t], [`+`(`/`(1, `*`(`^`(t, 11))), `/`(1, `*`(`...](images/FormalReductionMapleExamples_405.gif) |
(11.1) |
| > |