Example Version2-1 : This is a case where the exponential parts have (conjugated) algebraic coefficients 2x2 (mu=1, d=2, r=1) 

 

> A := rtable(1 .. 2, 1 .. 2, [[`/`(1, `*`(`^`(x, 5))), `/`(1, `*`(`^`(x, 5)))], [`/`(1, `*`(`^`(x, 5))), `/`(1, `*`(`^`(x, 4)))]], subtype = Matrix); -1; Exp_parts(A, x, t); 1
 

 

 

 

 

 

 

 

[Matrix(%id = 18446744078318386750), `+`(`*`(`^`(lambda, 2)), `*`(13, `*`(lambda)), 41)]
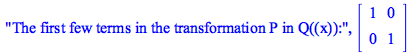The first few terms in the transformation P in Q((x)):
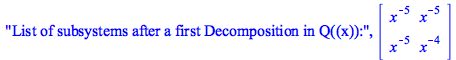List of subsystems after a first Decomposition in Q((x)):
A multiple of the ramification of each sub system:
We do elementary tranformations and apply the ramification when necessary.
[`+`(`/`(`*`(RootOf(`+`(`*`(`^`(_Z, 2)), `-`(_Z), `-`(1)))), `*`(`^`(t, 5))), `-`(`/`(`*`(`/`(1, 5), `*`(RootOf(`+`(`*`(`^`(_Z, 2)), `-`(_Z), `-`(1))))), `*`(`^`(t, 4)))), `/`(`*`(`/`(3, 5)), `*`(`^`(...
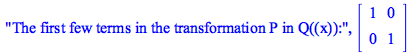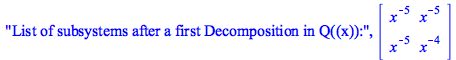[`+`(`/`(`*`(RootOf(`+`(`*`(`^`(_Z, 2)), `-`(_Z), `-`(1)))), `*`(`^`(t, 5))), `-`(`/`(`*`(`/`(1, 5), `*`(RootOf(`+`(`*`(`^`(_Z, 2)), `-`(_Z), `-`(1))))), `*`(`^`(t, 4)))), `/`(`*`(`/`(3, 5)), `*`(`^`(...		 (17.1)
 

>