Example V2-7: This is a case where we have two copies of conjuguates exponential parts by the action x-t^2=0 (mu=2,d=1,r=1)
| > | 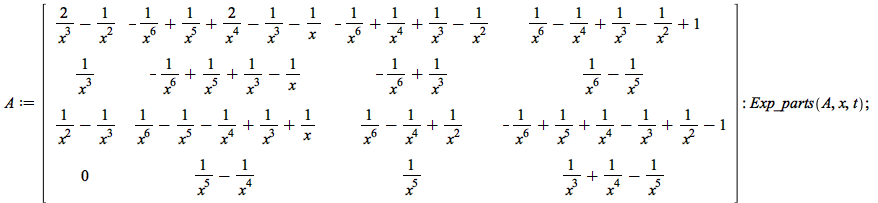 |
![[Matrix(%id = 18446744078322838494), `*`(`^`(`+`(`*`(`^`(lambda, 2)), lambda, 214), 2))]](images/FormalReductionMapleExamples_584.gif) |
|
 |
|
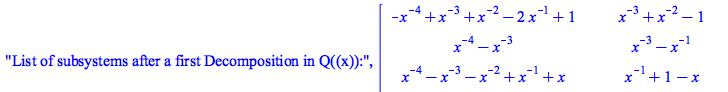 |
|
| (23.1) |
| > |
Example V2-7: This is a case where we have two copies of conjuguates exponential parts by the action x-t^2=0 (mu=2,d=1,r=1)
| > | 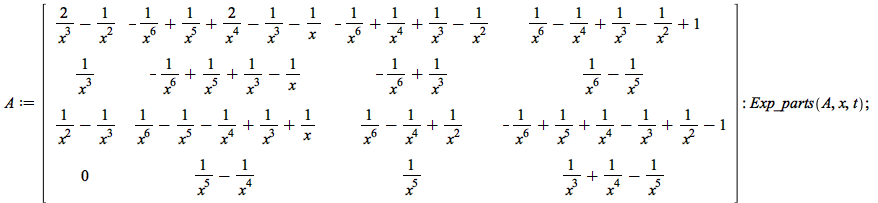 |
![[Matrix(%id = 18446744078322838494), `*`(`^`(`+`(`*`(`^`(lambda, 2)), lambda, 214), 2))]](images/FormalReductionMapleExamples_584.gif) |
|
 |
|
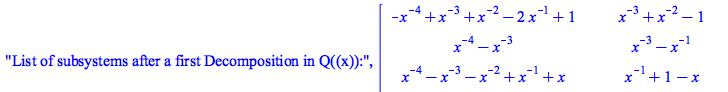 |
|
| (23.1) |
| > |