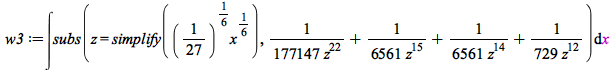Example 4 (ex. 15 and 16 in paper) New version 1 and 2
| > |
 |
| > |
 |
| > |
 |
| > |
 |
Version 1 (ex 15 in paper)
| > |
 |
| > |
 |
| > |
 |
![rtable(1 .. 2, 1 .. 2, [[`/`(1, `*`(`^`(x, 4))), 0], [0, `/`(1, `*`(`^`(x, 4)))]], subtype = Matrix)](images/FormalReductionMapleExamples_86.gif) |
(4.1.3) |
| > |
 |
 |
(4.1.4) |
| > |
 |
| > |
 |
| > |
 |
| > |
 |
| > |
 |
 |
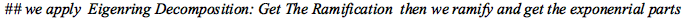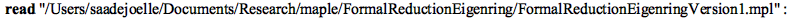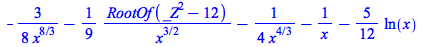(4.1.6) |
| > |
 |
 |
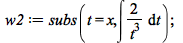(4.1.7) |
| > |
 |
 |
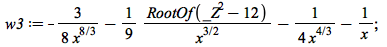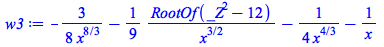(4.1.8) |
Version 2 (ex 16 in paper)
| > |
 |
| > |
 |
 |
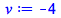(4.2.1) |
| > |
 |
| > |
 |
| > |
 |
 |
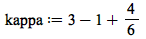(4.2.3) |
| > |
 |
| > |
![A := super_reduce(convert(A, polynom), t, t, u, 'T1', 'invT1')[1]; 1; v := Get_Valuation(A, t)](images/FormalReductionMapleExamples_132.gif) |
 |
 |
(4.2.4) |
| > |
 |
| > |
 |
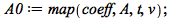![A0 := rtable(1 .. 6, 1 .. 6, [[0, 0, `+`(`-`(`/`(`*`(3), `*`(`^`(c, 2))))), 0, `+`(`-`(`/`(`*`(3), `*`(`^`(c, 2))))), 0], [`+`(`-`(`/`(`*`(3), `*`(`^`(c, 3))))), 0, 0, `+`(`/`(`*`(3), `*`(`^`(c, 2))))...](images/FormalReductionMapleExamples_137.gif) |
(4.2.5) |
| > |
 |
 |
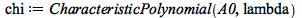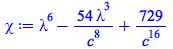(4.2.6) |
| > |
 |
 |
 |
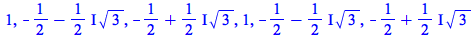(4.2.7) |
| > |
 |
 |
 |
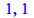(4.2.8) |
| > |
 |
| > |
 |
 |
 |
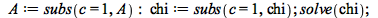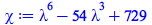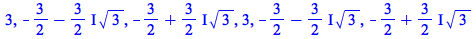(4.2.9) |
| > |
 |
| > |
 |
| > |
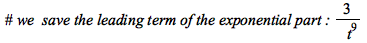![M := `+`(A, `-`(`/`(`*`(3, `*`(IdentityMatrix(6))), `*`(`^`(t, 9))))); -1; M := super_reduce(convert(M, polynom), t, t, u, 'T1', 'invT1')[1]; -1](images/FormalReductionMapleExamples_152.gif) |
| > |
 |
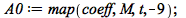![A0 := rtable(1 .. 6, 1 .. 6, [[-6, 0, -3, 0, 0, 0], [-5, -6, 0, 3, 0, 0], [3, 0, -3, 0, 0, 0], [-4, -3, -3, -3, 0, 0], [-3, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0]], subtype = Matrix)](images/FormalReductionMapleExamples_154.gif) |
(4.2.10) |
| > |
 |
 |
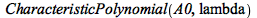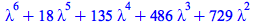(4.2.11) |
| > |
 |
 |
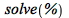(4.2.12) |
| > |
 |
| > |
 |
| > |
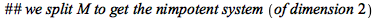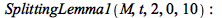![AA := map(convert, %[1], polynom); 1](images/FormalReductionMapleExamples_164.gif) |
 |
(4.2.14) |
| > |
 |
| > |
 |
| > |
 |
 |
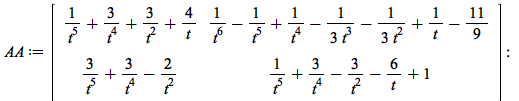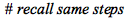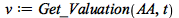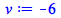(4.2.15) |
| > |
 |
| > |
 |
| > |
 |
 |
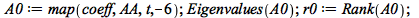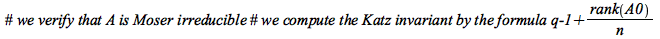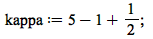(4.2.17) |
| > |
 |
| > |
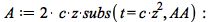![A := super_reduce(convert(A, polynom), z, z, u, 'T1', 'invT1')[1]; 1; v := Get_Valuation(A, z)](images/FormalReductionMapleExamples_178.gif) |
 |
 |
(4.2.18) |
| > |
 |
| > |
 |
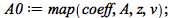![A0 := rtable(1 .. 2, 1 .. 2, [[0, `+`(`/`(`*`(6), `*`(`^`(c, 4))))], [`+`(`/`(`*`(2), `*`(`^`(c, 5)))), 0]], subtype = Matrix)](images/FormalReductionMapleExamples_183.gif) |
(4.2.19) |
| > |
 |
 |
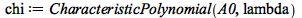(4.2.20) |
| > |
 |
 |
 |
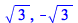(4.2.21) |
| > |
 |
 |
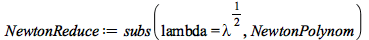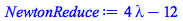(4.2.22) |
| > |
 |
 |
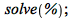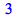(4.2.23) |
| > |
 |
| > |
 |
| > |
 |
 |
 |
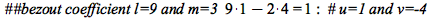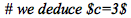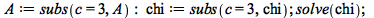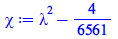(4.2.24) |
| > |
 |
| > |
![M := `+`(A, `-`(`/`(`*`(`/`(2, 81), `*`(IdentityMatrix(2))), `*`(`^`(z, 10))))); -1; M := super_reduce(convert(M, polynom), z, z, u, 'T1', 'invT1')[1]; -1](images/FormalReductionMapleExamples_199.gif) |
| > |
 |
![A0 := rtable(1 .. 2, 1 .. 2, [[-`/`(4, 81), 0], [`/`(2, 243), 0]], subtype = Matrix)](images/FormalReductionMapleExamples_201.gif) |
(4.2.25) |
| > |
 |
 |
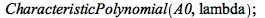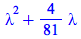(4.2.26) |
| > |
 |
 |
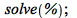(4.2.27) |
| > |
 |
| > |
 |
| > |
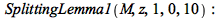![AA := map(convert, %[1], polynom); 1](images/FormalReductionMapleExamples_211.gif) |
![AA := rtable(1 .. 1, 1 .. 1, [[`+`(`/`(`*`(`/`(2, 81)), `*`(`^`(z, 9))), `/`(`*`(`/`(2, 9)), `*`(`^`(z, 7))), `-`(`/`(`*`(`/`(5, 2)), `*`(z))))]], subtype = Matrix)](images/FormalReductionMapleExamples_212.gif) |
(4.2.29) |
| > |
 |
| > |
 |
 |
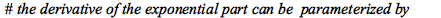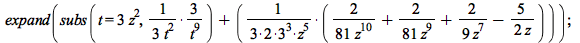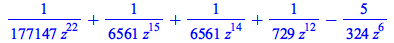(4.2.30) |
| > |
 |
| > |
 |
 |
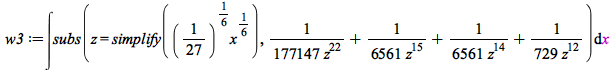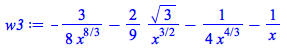(4.2.32) |
![A0 := rtable(1 .. 9, 1 .. 9, [[1, 0, 1, -1, 0, 0, 0, 1, 1], [-1, 1, -1, 0, 0, 0, 1, 0, -1], [0, 0, 0, 0, 0, 0, 0, 0, 0], [-1, 0, -1, 1, 0, 0, 0, -1, -1], [1, 0, 0, 1, 0, 0, 0, 0, 0], [1, -1, 1, 0, 0, ...](images/FormalReductionMapleExamples_72.gif)
![rtable(1 .. 9, [1, 1, 0, 0, 0, 0, 0, 0, 0], subtype = Vector[column])](images/FormalReductionMapleExamples_73.gif){kind=small}
![{rtable(1 .. 9, [-1, 0, 0, 0, 0, 0, 0, 1, 0], subtype = Vector[column]), rtable(1 .. 9, [0, -1, 0, 0, 0, 0, 1, 0, 0], subtype = Vector[column]), rtable(1 .. 9, [0, 0, 0, 0, 0, 0, 0, 0, 1], subtype = V...](images/FormalReductionMapleExamples_76.gif)
![[Matrix(%id = 18446744078318383102), `*`(`+`(lambda, `-`(9)), `*`(`^`(`+`(lambda, `-`(5)), 6)))]](images/FormalReductionMapleExamples_101.gif)
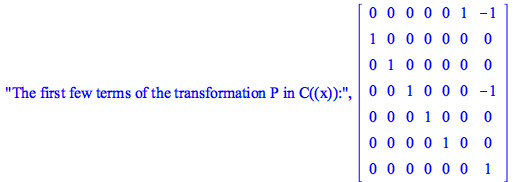
![A0 := rtable(1 .. 6, 1 .. 6, [[0, 0, 0, 0, 1, -1], [-1, 0, 0, 0, 0, 1], [0, 1, 0, 0, 0, 1], [-1, 0, 0, 0, 1, 0], [0, 0, 0, 0, 1, -1], [0, 0, 0, 1, 1, -1]], subtype = Matrix)](images/FormalReductionMapleExamples_125.gif)
![rtable(1 .. 6, [0, 0, 0, 0, 0, 0], subtype = Vector[column])](images/FormalReductionMapleExamples_126.gif){kind=small}
![rtable(1 .. 6, 1 .. 6, [[-6, 0, -3, 0, 0, 0], [-5, -6, 0, 3, 0, 0], [3, 0, -3, 0, 0, 0], [-4, -3, -3, -3, 0, 0], [-3, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0]], subtype = Matrix)](images/FormalReductionMapleExamples_161.gif)
![A0 := rtable(1 .. 2, 1 .. 2, [[0, 1], [0, 0]], subtype = Matrix)](images/FormalReductionMapleExamples_171.gif)
![rtable(1 .. 2, [0, 0], subtype = Vector[column])](images/FormalReductionMapleExamples_172.gif){kind=small}
![rtable(1 .. 2, 1 .. 2, [[-`/`(4, 81), 0], [`/`(2, 243), 0]], subtype = Matrix)](images/FormalReductionMapleExamples_208.gif)
