Example : Example 3.6 in paper "A new approach for formal reduction of singular linear
differential systems using eigenrings".
| > | ![A := `/`(`*`(rtable(1 .. 4, 1 .. 4, [[0, 0, x, 0], [1, `+`(`-`(`*`(`^`(x, 2)))), `*`(`^`(x, 2)), `+`(`-`(`*`(`^`(x, 2))))], [0, 1, `*`(`^`(x, 2)), 0], [`*`(`^`(x, 2)), `*`(`^`(x, 2)), 0, `+`(`-`(`*`(`...](images/FormalReductionMapleExamples_307.gif) |
| > |
![[rtable(1 .. 4, 1 .. 4, [[`+`(`-`(1), O(`*`(`^`(x, 5)))), O(`*`(`^`(x, 4))), O(`*`(`^`(x, 4))), `+`(`-`(`*`(`^`(x, 2))), O(`*`(`^`(x, 5))))], [O(`*`(`^`(x, 8))), `+`(`-`(1), O(`*`(`^`(x, 7)))), O(`*`(...](images/FormalReductionMapleExamples_311.gif) |
|
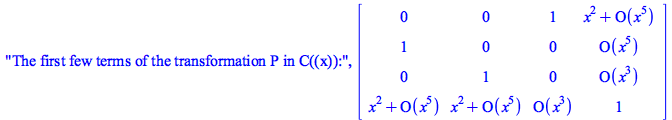 |
|
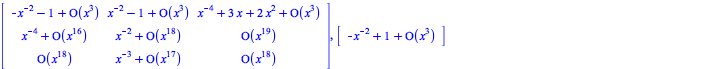 |
|
![[`+`(`/`(1, `*`(`^`(t, 11))), `/`(`+`(`*`(3, `*`(`^`(t, 7))))), `-`(`/`(`+`(`*`(3, `*`(`^`(t, 3))))))), x = `*`(`^`(t, 3))], [rtable(1 .. 1, 1 .. 1, [[`+`(`-`(`/`(1, `*`(`^`(t, 2)))))]], subtype = Mat...](images/FormalReductionMapleExamples_320.gif) |
(6.1) |
| > |
| > |
| > | 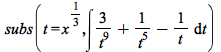 |
| (6.2) |
| > |
| > |
| (6.3) |
| > |
| (6.4) |
| > |
Example : Example 3.6 in paper "A new approach for formal reduction of singular linear
differential systems using eigenrings".
| > | ![A := `/`(`*`(rtable(1 .. 4, 1 .. 4, [[0, 0, x, 0], [1, `+`(`-`(`*`(`^`(x, 2)))), `*`(`^`(x, 2)), `+`(`-`(`*`(`^`(x, 2))))], [0, 1, `*`(`^`(x, 2)), 0], [`*`(`^`(x, 2)), `*`(`^`(x, 2)), 0, `+`(`-`(`*`(`...](images/FormalReductionMapleExamples_307.gif) |
| > |
![[rtable(1 .. 4, 1 .. 4, [[`+`(`-`(1), O(`*`(`^`(x, 5)))), O(`*`(`^`(x, 4))), O(`*`(`^`(x, 4))), `+`(`-`(`*`(`^`(x, 2))), O(`*`(`^`(x, 5))))], [O(`*`(`^`(x, 8))), `+`(`-`(1), O(`*`(`^`(x, 7)))), O(`*`(...](images/FormalReductionMapleExamples_311.gif) |
|
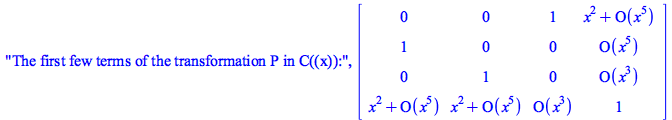 |
|
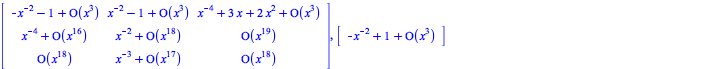 |
|
![[`+`(`/`(1, `*`(`^`(t, 11))), `/`(`+`(`*`(3, `*`(`^`(t, 7))))), `-`(`/`(`+`(`*`(3, `*`(`^`(t, 3))))))), x = `*`(`^`(t, 3))], [rtable(1 .. 1, 1 .. 1, [[`+`(`-`(`/`(1, `*`(`^`(t, 2)))))]], subtype = Mat...](images/FormalReductionMapleExamples_320.gif) |
(6.1) |
| > |
| > |
| > | 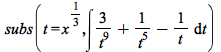 |
| (6.2) |
| > |
| > |
| (6.3) |
| > |
| (6.4) |
| > |