Hungarian Algorithm

   A Maple package for computing a tropical determinant (solving assignment problem).


   
Author: J. Saade

I - Introduction

We want to assign n jobs to n different employees so that all jobs are assigned and exactly one person is assigned to each job and exactly one job is assigned to each person. Each assignment employee-job incurs some cost. Solving the assignment problem is to minimize the total cost of the assignment. The naïve method is to generate n! possible job assignments and for each such assignment we compute the total cost. Therefore, the complexity is O(n!).
The Hungarian method is an algorithm for solving the assignment problem. Its worst case run-time complexity is O(n^3).
References:
Algorithms for the assignment and transportation problems (James, Munkres).
The Hungarian method for the assignment problem (Kuhn, Harold W).
A new implementation of an algorithm for the optimal assignment problem: An improved version of Munkres' algorithm (Wong, Jin Kue).

"Solving the assignment problem with Hungarian method".

II - Download and installation

Our package is available for download: HungarianAlgorithm.m

To install it, you must proceed as follows:
  1. Set up a directory to store your custom library as explained in Maple Programming Guide
  2. Copy the previous HungarianAlgorithm.m file in a directory called "HungarianAlgorithm"
  3. Open Maple and read  

    read "the global path of the directory     HungarianAlgorithm.m";

    example : read("/Users/saadejoelle/Desktop/HungarianAlgorithm/HungarianAlgorithm.m");

  4. After that type

    savelib('HungarianAlgorithm');

  5. Type

    restart; with(HungarianAlgorithm);

You must get the list of the three functions contained in the package: [BruteForce, LenghtOfMinimalPath, MinimalPathWithHungarian]

If you do not manage to install the package, then contact us.

III - The procedures

  1. MinimalPathWithHungarian, LenghtOfMinimalPath

    Given R:=(r_{ij})an n\times n matrix with postive entries, the MinimalPathWithHungarian computes the minimal path 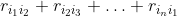. If (r_{ij}) represents the cost of assignment of the jobs i to the worker j, the function MinimalPathWithHungarian gives the total minimized assignment.
    The output is an n\times n matrix M:=(m_{ij}) where m_{ij}=1 if the job i is assigned to the worker j and 0 if not.
    The procedure LenghtOfMinimalPath computes the minimal cost       \sum_{i=1}^{n}\sum_{j=1}^{n}r_{ij}m_{ij}.      

  2. Brute Force

    The naïve method: generate n! possible job assignments and for each such assignment compute the total cost. Finally, consider the minimal cost between these n! quatities.      

  3. Example session